You need to use hark_msgs/HarkWave in your workspace.
In your case, audio_common_msgs/AudioData seems to store mp3 data into uint8[] array, so you will first need to expand it to raw PCM data.
Second, the data structure of hark_msgs/HarkWave is as follows.
user@ubuntu:~$ rosmsg show hark_msgs/HarkWave
std_msgs/Header header
uint32 seq
time stamp
string frame_id
int32 count
int32 nch
int32 length
int32 data_bytes
hark_msgs/HarkWaveVal[] src
float32[] wavedatawavedata is a raw PCM data array. Since HARK is not aware of the number of bits, it simply casts an integer value to a floating point type. In other words, 123 is 123.0f .
data_bytes is the data size. In other words, it is the size of float (4 bytes) multiplied by the size of wavedata .
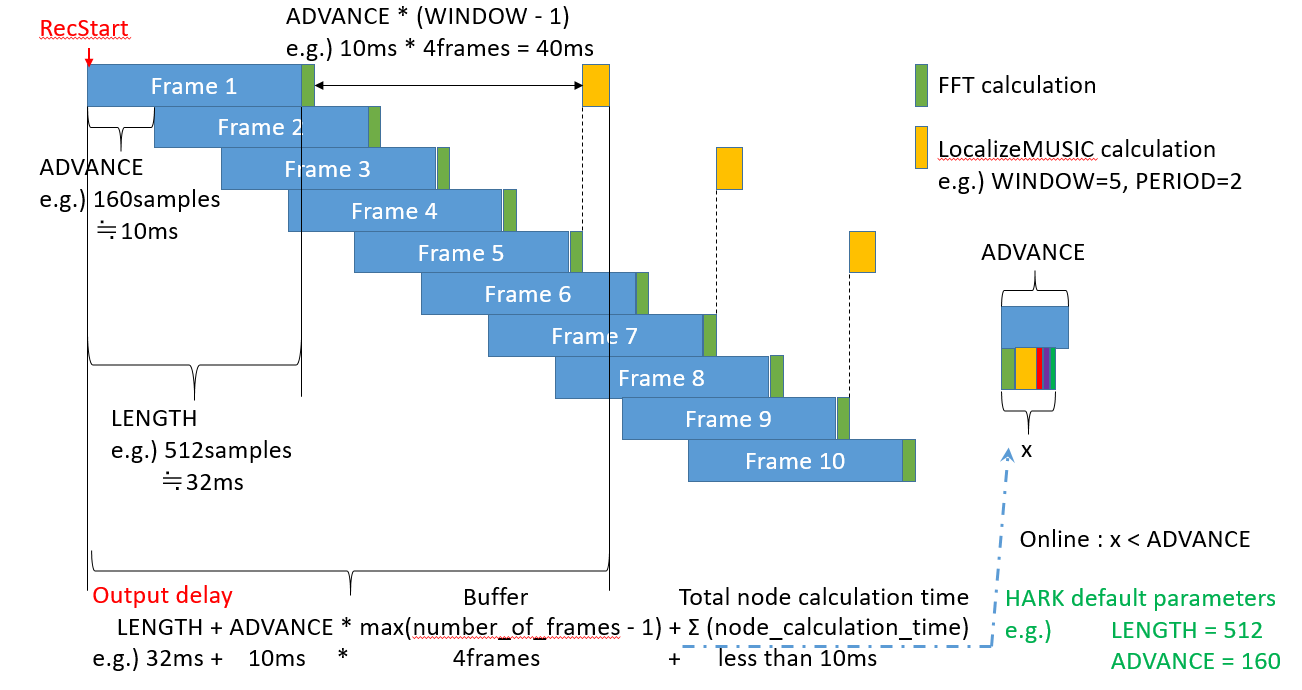
length is the number of samples per frame handled by HARK. The initial value of HARK is 512 . Since HARK processed frame by frame, in other words, the size of wavedata must be nch times length=512 .
nch is the number of channels. Your device seems to be 1ch, so it should be 1 . For microphone array data, a larger number will be stored.
count is the frame count. Since HARK processing frame by frame, it is necessary to know what frame the data is. In other words, it is incremented as the frame advances. The first frame number is 0 . Not 1 .
There is a final note. In order to prevent problems in FFT/IFFT processing, etc., the frames processing by HARK are subject to sample overlap processing.
The following image may help you understand.
Best regards,
m.takigahira